Years of Learning

Damian Betebenner

Santa Fe, New Mexico

May 23rd, 2023

Apples by the bushel,

learning by the year!

{sept }§0y|0e|0a|1r|1[+]s|1[+] |1o|1[+]f|2 |2l|2[+]e|2a|2r|2n|3i|3n|3g|3{june }

• Expressions relating amounts of learning to time (e.g., a year’s worth of learning) have been around for a long time.¹
• These expressions often roll off the tongue and suggest something obvious – something that everyone understands.²
• Despite the commonsense facade, relating amount of learning to time conceals significant technical and conceptual issues.
• I would argue that the expression On grade level is to attainment as a year’s worth of learning is to growth.

1. When going through some old documents I found a paper and presentation I wrote for AERA on the topic back in 2008 that I had completely forgotten about.

2. Think of the expression an honest day’s work.

Inspiration

• Pandemic Related Insights
  • Reporting of pandemic learning loss: Weeks/months/years of lost learning.
  • Recognition of learning being a process with an inherent velocity
• Sandy Student’s NCME presentation (2023) and discussion on year’s worth of learning (his dissertation topic).
• Strategic planning by states including updates long term achievement targets
  • Desire to calibrate achievement indicators to ambitious yet reasonable individual learning/growth goals (Hawaii and Rhode Island).
  • Recent staff sharing from Brian on work in Kentucky related to accountability systems.
• Desire to make rigorous “a year’s worth of learning” in order to better communicate SGP results.

My Personal Perspectives/Biases

• Communicating results to non-technical audiences requires trade-offs.
• The best solution from a technical perspective may be a communication failure from a practical perspective.
• Utility trumps validity.
• Are the shortcomings of expressions like year’s worth of learning so large as to make them counterproductive?
• One prominent researcher in the measurement field doesn’t think so.

Andrew Ho’s Rule of 27

1

2

:::::

Education is not the filling of a pail, but the lighting of a fire.

William Butler Yeats

Fons Sapientiae Leuven, Belgium

The name translates to “Source of Wisdom,” and the water the man pours atop his head is supposedly meant to symbolize knowledge flowing into his brain. An intricate math formula is scrawled across the front cover of the book he clutches that, when solved, forms the Dutch word for “happiness.”

• The predominant view of learning and education (IMHO).
• Volume/amount of “learning” delivered to students in a given time.
  • Weeks, months, years of learning.
• Time on task

• Inspirational, but is this reality?
• Would we know fire if we saw it?
  • How would fire manifest itself in assessment results?

Understanding change

Cross-Sectional Change (Improvement)

• Comparison of same grade and content area over time
• Often used to examine changes in percent proficient
• Most common comparison utilized for large scale assessment data

Longitudinal Change (Growth)

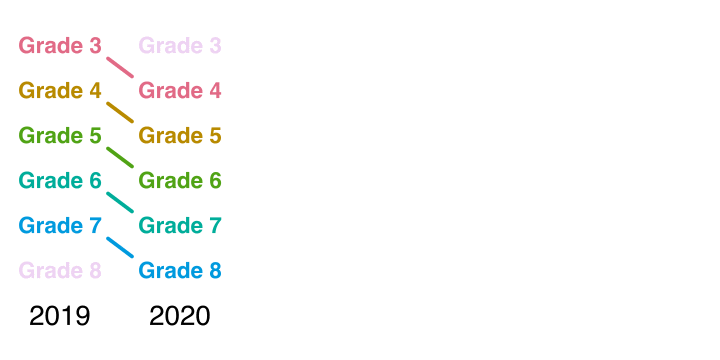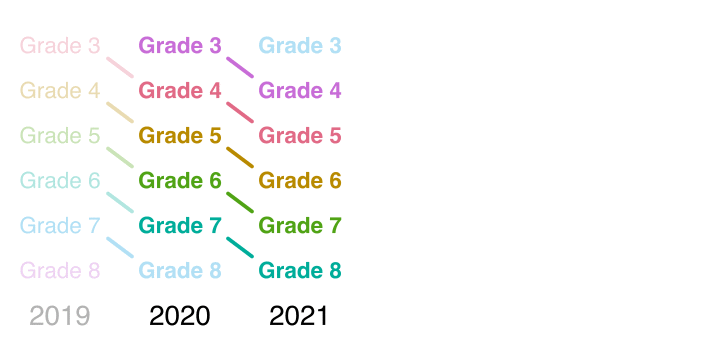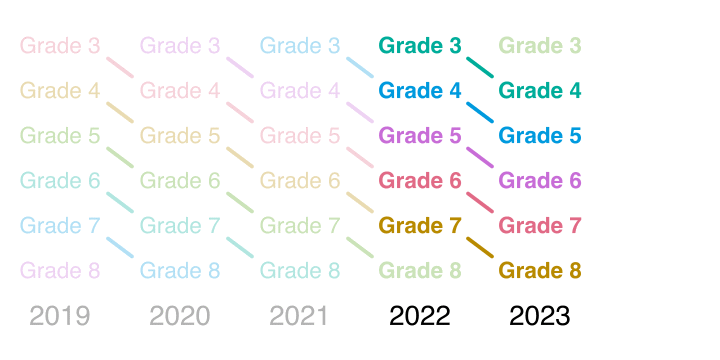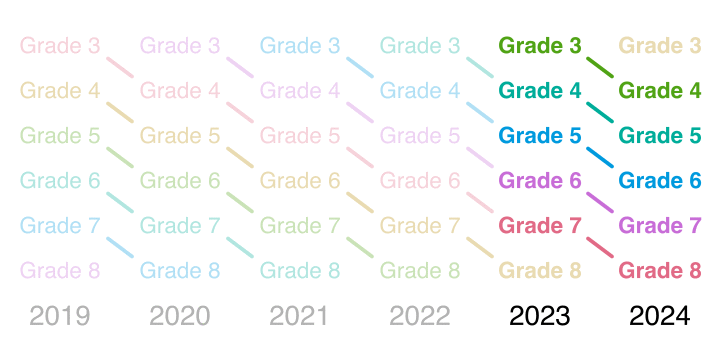
• Examine change of cohort of same students over time
• Data structure used to calculate student growth (e.g., SGPs)
• Calculation of magnitude of change requires a vertical scale.
• This is the data structure associated with years of learning.

A Year’s Worth of Learning

• A year’s worth of learning purports to express an amount of growth (i.e., learning) demonstrated by students.
• The quantity can be construed as the effect due to exposure of a year’s worth of education.
• Bloom et al. (2008) compare effect sizes to estimates of how much students grow in one year.
• Dadey and Briggs (2012) investigated the extent to which design and content differences impact growth trends on vertically scaled assessments

Years of Learning: A Question

Effect Size

• Following Yen (1986) and Dadey and Briggs (2012) cross-grade, effect size is defined as the standardized mean difference between grade x content area means (\(g1\) and \(g2\)) using the pooled standard deviation:

\[ \textsf{Effect Size} \equiv \frac{\overline{X}_{g1} - \overline{X}_{g2}}{\sqrt{\frac{\hat{ \sigma}^2_{g1} + \hat{ \sigma}^2_{g2}}{2}}} \tag{1}\]

• Note, in order for this mean difference in the numerator to make sense, we must have a scale (i.e., a vertical scale or developmental scale) that allows for the subtraction of scaled scores.
• The effect size quantifies the extent to which the mean has shifted between the two scaled score distributions.
• There will be considerable overlap in the students in \(g1\) and \(g2\) in most applications of Equation 1 to state summative assessment data. However, there is no requirement that \(g1\) and \(g2\) consist of the same students (e.g., NAEP).

Effect Size Illustration

• Figure shows effect size for matched grade 3 to 4 students in mathematics.
• Mean scaled score increase of 35 (461 to 496).
• Effect size increase of 0.41.
• Note: This effect size change is applicable to the entire group of students but not, in general, to individual students.
• Why?

Effect Size Illustration

• Increase in attainment is not uniform by prior attainment (i.e., gains correlate with initial achievement).
• Figure shows two regions:
  • Individual gains above effect size.
  • Individual gains below effect size.
• Bottom axis includes decile cuts for Grade 3 scaled score.
• In lowest decile, 74.4% of students had gains exceeding the effect size. In highest decile, 15.7% had gains exceeding the effect size.
• Reductio ad absurdum

Empirical results

• We examine effect size increases for unmatched and matched cohorts of students using data from 4 states.
• All data are derived from assessment administrations occurring prior to the COVID-19 pandemic.
• Using Equation 1 we calculate effect size changes for 1, 2, 3, and 4 years (provided enough years of data exist for the state).
• Depending upon the number of years of data we have for a state, we can calculate effect size changes across several cohorts of students.
• Results are summarized in the following figures.

Mathematics

• State A
• State B
• State C
• State D

ELA

• State A
• State B
• State C
• State D

Let’s Summarize

• The effect size approach to quantifying a year’s worth of learning depends on:
  • the assessment that is administered,
  • the population of students to whom the assessment is administered,
  • the year in which the assessment is administered,
  • the content area of the assessment,
  • the grade level of the assessment, and
  • the psychometric design used to scale and construct the assessment.
  • Moreover, the calculated effect size is only a system level average and is not applicable for determinations of a year’s worth of learning at the individual level.
• This list of dependencies is as bad as the list we’d put together for any indicator derived from assessments.
  

Yikes!!!

• Hard to call this rule anything but just BAD
• The assumptions (3 grade levels per standard deviation) don’t hold.
• Gives rise to misleading statements, especially for parents concerned about their children.
  
• Not good. We should do better.

Rule of 27

:::::

Is there any

Yes!

• Mean
• Conditional Mean
• Conditional Median
• Conditional Decile

How?

• Year’s worth of learning is implicitly a norm-referenced quantity based upon average student performance.
• As such, one can employ regression based approaches to better formalize the concept.
• Attempts to reduce a year’s worth of learning to an effect size are a clumsy, scaled-based attempt to address the question.
• As a norm-referenced quantity, SGPs can be utilized to define a year’s worth of learning to be 50th percentile growth.
• This is consistent with the effect size approach to defining change and avoids all of the shortcomings mentioned.
• The next section explores the consequences of this.

SGP & Years of Learning

• We investigate the relationship between growth norms and year’s of learning.
• To do so, we exploit the the properties of the vertical scale.
  • A vertical scale purports to produce a score scale capable of providing comparable, cross-grade, scaled scores for a given content area across the range of achievement.
  • For example, a vertical scale support scale score subtraction.
• The goal is to quantify year’s of learning in terms of an SGP.
  • What SGP is associated with 2 years of learning?
  • What SGP is associated with 3 years of learning?
  • What SGP is associated with no learning (or zero years of learning).

Analyses

• We examine the relationship between mean SGP and year’s of learning using pre-pandemic, vertically scaled, pre-pandemic, longitudinal data from 4 states as follows:
  • One year’s growth (for a one year span of time) is defined as 50th percentile growth. This is a normal SGP.
  • Two year’s growth (in one year) is calculated empirically by running individual data spanning two years (e.g. grade 3 to 5 data) through one-year growth norms (e.g., grade 3 to 4 growth norms).
  • Three year’s growth (in one year) is calculated empirically by running individual data spanning three years (e.g. grade 3 to 6 data) through one-year growth norms (e.g., grade 3 to 4 growth norms).
  • No growth (in one year) is calculated by running individual data with no increase in scaled score through the one-year growth norms (e.g., grade 3 to 4 growth norms).
  • I also calculated half-year growth (in one year) by running individual data spanning a single year (e.g., grade 3 to 4 data) through two-year growth norms(e.g., grade 3 to 5 growth norms).
• Results are summarized in the following figures.

SGP by Years of Learning: Mathematics

• State A
• State B
• State C
• State D

SGP by Years of Learning: ELA

• State A
• State B
• State C
• State D

Back to the survey question

• Based upon the SGP analyses were you able to determine the correct answer to the question you answered?

Startling results

• The results perplexed me when I ran the analyses a month ago.
• How is it possible for 60 or more percent of students making at least a year’s worth of learning to make two or more year’s worth of learning.
  • Are vertical scales this corrupt?
  • Charlie DePascale called vertical scaling an interesting parlor trick.

Summary thoughts (preliminary)

• Years of learning interpretations based upon effect-size calculations are a dead end.
• It’s not clear whether extending the effect size approach to utilize growth norms leads to coherent results.
  • It’s too easy to throw vertical scales under the bus. For adjacent grades, scaled scores should be close to exchangable.
• The possibility that student learning could be so “explosive” after reaching the year of learning threshold could have huge implications for educating students.
• I want to believe there is a way to approximately map learning rates to time.

Questions?

Project Website

Presentation

Bloom, Howard S., Carolyn J. Hill, Alison Rebeck Black, and Mark W. Lipsey. 2008. “Performance Trajectories and Performance Gaps as Achievement Effect-Size Benchmarks for Educational Interventions.” Journal of Research on Educational Effectiveness 1 (4): 289–328. https://doi.org/10.1080/19345740802400072.

Dadey, Nathan, and Derek Briggs. 2012. “A Meta-Analysis of Growth Trends from Vertically Scaled Assessments.” Practical Assessment, Research & Evaluation 17 (December).

R.Student, Sanford. 2023. “What’s in a Year: Updated Annual Growth Trends on Vertically Scaled Tests.” Presentation made at the 2023 NCME Conference, Chicago, IL, April, 2023.

Yen, Wendy M. 1986. “The Choice of Scale for Educational Measurement: An IRT Perspective.” Journal of Educational Measurement 23: 299–325.